ESPIRAL DE FIBONACCI / PROPORÇÃO ÁUREA

Sequência de Fibonacci (Proporção Aurea).

É uma sucessão de números que, aparece em muitos fenômenos da natureza. Descrita no final do século 12 pelo italiano Leonardo Fibonacci, ela é infinita e começa com 0 e 1. Os números seguintes são sempre a soma dos dois números anteriores. Portanto, depois de 0 e 1, temos 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657... Ao transformar esses números em quadrados e dispô-los de maneira geométrica, é possível traçar uma espiral perfeita, que também aparece em diversos organismos vivos. Outra curiosidade é que os termos da sequência também estabelecem a chamada “proporção áurea”, muito usada na arte, na arquitetura e no design por ser considerada agradável aos olhos. Seu valor é de 1,618 e, quanto mais se avança na sequência de Fibonacci, mais a divisão entre um termo e seu antecessor se aproxima desse número.

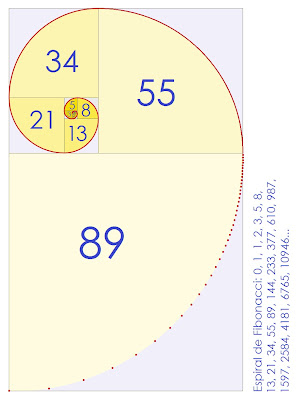
Espiral de Fibonacci.

Sequência de Fibonacci, espiral de Fibonacci e proporção áurea.

Solve y = ( 1 + 1/x ) results φ = 1,618 and φ's little brother = - 0,618.

Exemplos em que a sequência ou espiral de Fibonacci aparece na natureza:

CONCHA DO CARAMUJO
Cada novo pedacinho tem a dimensão da somados dois antecessores.

GIRASSOL / PINHA
No girasol as suas sementes preenchem o miolo dispostas em dois conjuntos de espirais: geralmente, 21 no sentido horário e 34 no anti-horário. As sementes de pinha crescem e se organizam em duas espirais que lembram a de Fibonacci: oito irradiando no sentido horário e 13 no anti-horário.

CAMALEÃO
Contraído, seu rabo é uma das representações mais perfeitas da espiral de Fibonacci.

POEMA
O “número de ouro” está presente até na razão entre as estrofes maiores e menores da Ilíada, épico de Homero sobre os últimos dias da Guerra de Troia.

PARTENON
Os gregos já conheciam a proporção, embora não a fórmula para defini-la. A largura e a altura da fachada deste templo do século V a.C. estão na proporção de 1 para 1,618.

GRANDES PIRÂMIDES
Mais um mistério: cada bloco é 1,618 vezes maior que o bloco do nível imediatamente acima. Em algumas, as câmaras internas têm comprimento 1,618 vezes maior que sua largura.

ARTES
Esse recurso matemático também foi uma das principais marcas do Renascimento. A Mona Lisa, de Leonardo da Vinci, usa a razão na relação entre tronco e cabeça e entre elementos do rosto.

A BELEZA DESCRITA EM NÚMEROS
A “Proporção de ouro” aparece tanto em seres vivos quanto em criações humanas. Na matemática, a razão dourada é representada pela letra grega phi: φ.

ELEFANTE
Se suas presas de marfim crescessem sem parar, ao final do processo o formato seria o da espiral de Fibonacci.

OBJETOS DO COTIDIANO
Vários formatos de cartão de crédito já foram testados. O que se sagrou favorito do público têm laterais na razão de ouro. Fotos e jornais também costumam adotá-la.

ROSTO / CORPO / MÃOS
Dizem que, nas faces consideradas mais harmoniosas, a divisão da distância entre o centro dos lábios e o “terceiro olho” pela distância entre esse ponto e uma das pupilas bate no 1,618. Se um humano “mediano” dividir sua altura pela distância entre o umbigo e a cabeça, o resultado será algo em torno de 1,618. Nas mãos, com exceção do polegar, em todos os outros dedos as articulações se relacionam na razão áurea.

Proporção áurea 1,618 - 0,618, triângulo isóceles, espiral, pentagrama e ângulos.

Cálculo para proporção áurea.

Proporção Áurea: definição algébrica.

Triângulo de ouro.

1   2   3   5   8   13   21   34   55   89   144   233   377   610   987   1597