Na comunicação de resultados de medição em ciências exatas, há regras de como expressar números e valores de grandeza, algarismos significativos, truncamento e arredondamento de números e algarismos significativos na incerteza padrão.
Expressando Número e Valor de uma Grandeza
Expressando um Número
Números com mais de quatro dígitos à direita da vírgula decimal devem ser separados por um espaço em grupos de três dígitos, com a restrição de que o último grupo não pode ter apenas um dígito. Exemplo: 1,123; 1,123.4; 1,123.45; 1,123.456; 1,123.456.7; 1,123.456.78; 1,123.456.789; etc.
Expressando o Valor de uma Grandeza
Números com mais de quatro dígitos à esquerda da vírgula decimal devem ser separados por um espaço em grupos de três dígitos, com a restrição de que primeiro grupo não pode ter apenas um dígito. Exemplo: 1,123; 11,234; 112,345; 1.123,456; 11.234,567; 112.345,678; 1.123.456,789; 11.234.567,890; etc.
Digita-se o número corresponde ao valor da grandeza seguido sem espaço do símbolo ± novamente sem espaço e o valor da incerteza seguido de espaço e do símbolo da unidade correspondente; ou
Digita-se o número correspondente ao valor da grandeza seguido dos dígitos significativos da incerteza entre parênteses seguido de espaço e do símbolo da unidade correspondente (de modo geral economiza a tarefa de digitação):
Algarismos Significativos
A precisão do resultado de uma grandeza obtida em um experimento está associada ao número de dígitos que compõe o valor numérico associada a ela. O número de dígitos significativos é definido como (Bevington);
Instrumento de precisão - Paquímetro (grego: paqui = espessura e metro = medida), por vezes também chamado de craveira em Portugal, é um instrumento utilizado para medir a distância entre dois lados simetricamente opostos em um objeto. Um paquímetro pode ser tão simples como um compasso. O paquímetro é ajustado entre dois pontos, retirado do local e a medição é lida em sua régua. O nônio ou vernier é a escala de medição contida no cursor móvel do paquímetro, que permite uma precisão decimal de leitura através do alinhamento desta escala com uma medida da régua.
1: encostos, 2: orelhas, 3: haste de profundidade, 4: escala inferior (graduada em mm), 5: escala superior (graduada em polegadas), 6: nônio ou vernier inferior (mm), 7: nônio ou vernier superior (polegada), 8: trava.
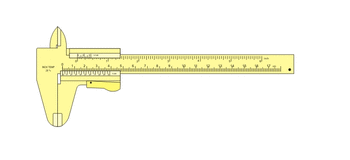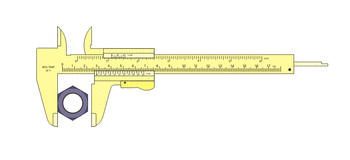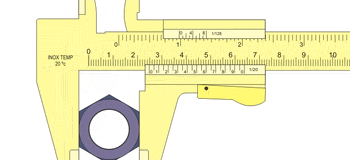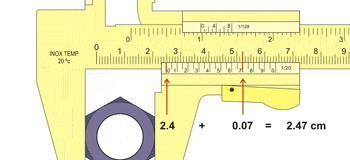
Uso de um Paquímetro.
Expressando Número e Valor de uma Grandeza
Expressando um Número
Números com mais de quatro dígitos à direita da vírgula decimal devem ser separados por um espaço em grupos de três dígitos, com a restrição de que o último grupo não pode ter apenas um dígito. Exemplo: 1,123; 1,123.4; 1,123.45; 1,123.456; 1,123.456.7; 1,123.456.78; 1,123.456.789; etc.
Expressando o Valor de uma Grandeza
Números com mais de quatro dígitos à esquerda da vírgula decimal devem ser separados por um espaço em grupos de três dígitos, com a restrição de que primeiro grupo não pode ter apenas um dígito. Exemplo: 1,123; 11,234; 112,345; 1.123,456; 11.234,567; 112.345,678; 1.123.456,789; 11.234.567,890; etc.
Digita-se o número corresponde ao valor da grandeza seguido sem espaço do símbolo ± novamente sem espaço e o valor da incerteza seguido de espaço e do símbolo da unidade correspondente; ou
Digita-se o número correspondente ao valor da grandeza seguido dos dígitos significativos da incerteza entre parênteses seguido de espaço e do símbolo da unidade correspondente (de modo geral economiza a tarefa de digitação):
- 18,010±0, 011 m ou 18,010(11) m
- (18 010±11) · 103 mm ou 18 010(11) · 103 mm
- 1.801,0±1,1 m ou 1.801,0(11) m
- 1,801.0±0,0011 km ou 1,801.0(11) km
Algarismos Significativos
A precisão do resultado de uma grandeza obtida em um experimento está associada ao número de dígitos que compõe o valor numérico associada a ela. O número de dígitos significativos é definido como (Bevington);
1 - O dígito não zero mais à esquerda em um número é o dígito mais significativo;
2 - Se não há vírgula decimal, o dígito não zero mais à direita é o menos significativo;
3 - Se há vírgula decimal, o dígito mais à direita é o menos significativo, mesmo que seja 0; e
4 - Todos os dígitos entre os dígitos mais significativo e menos significativos são nomeados dígitos significativos.
Truncamento e Arredondamento
decimal. Regras de arredondamento:
1 - Se a fração decimal dos dígitos omitidos for maior que 1/2, o dígito menos significativo é aumentado de uma unidade;
2 - Se a fração decimal dos dígitos omitidos for menor que 1/2, o dígito menos significativo permanece inalterado; e
3 - Se a fração decimal dos dígitos omitidos for igual a 1/2, o dígito menos significativo é aumentado de uma unidade caso ele seja ímpar, caso contrário permanece com o mesmo valor.
0,011.475.0 → 0,011.48 justificativa 0,50 = 1/2 e 7 é ímpar
0,011.465.0 → 0,011.46 justificativa 0,50 = 1/2 e 6 é par
0,011.475 → 0,011.5 justificativa 0,75 > 1/2
0,011.475 → 0,01 justificativa 0,147.5 < 1/2
Compare o arrendondamento do valor da carga do elétron deste quadro com os resultados de truncamento:
Algarismos Significativos na Incerteza Padrão
Segundo Vanin, Gouffon e Helene as regras para o número de algarismos na incerteza padrão de uma medição são:
1 - A incerteza padrão deve ser apresentada com dois algarismos significativos quando o primeiro algarismo significativo do valor da incerteza for o dígito um ou o dígito dois; e
2 - A incerteza padrão pode ser apresentada com um ou dois algarismos significativos quando o primeiro algarismo significativo do valor da incerteza for o dígito três ou maior.
O valor obtido para uma medição foi média de 18,010.200 e incerteza padrão de 0,011.475.
Como a incerteza padrão deve ser apresentada por dois algarismos significativos na situação em que o dígito mais significativo do número é 1 tem-se que:
3 - Se há vírgula decimal, o dígito mais à direita é o menos significativo, mesmo que seja 0; e
4 - Todos os dígitos entre os dígitos mais significativo e menos significativos são nomeados dígitos significativos.
- 1.024 – 4 significativos
- 1,024 – 4 significativos
- 0,025 – 2 significativos
- 0,200.0 – 4 significativos
- 1,602.176.563·10-19 – 10 significativos (carga do elétron em C)
- 8,854.187.817·10-19 – 10 significativos (permitividade elétrica no vácuo em F/m)
- 25·10-3 – 2 significativos
- 200 – 3 significativos
- 20,0 – 3 significativos
- 0,200 – 3 significativos
Truncamento e Arredondamento
Truncamento
Truncar um valor é diminuir o número de dígitos que o constitui sem se preocupar com a precisão que ele representa:
Arredondamento
Resultados experimentais devem ser apresentados com o número de dígitos significativos de acordo com a precisão experimental que se tem. Assim, trunca-se o resultado para ter o número de dígitos pretendido, levando em conta os dígitos omitidos como uma fraçãoTruncar um valor é diminuir o número de dígitos que o constitui sem se preocupar com a precisão que ele representa:
- 1,602.176.563·10-19
- 1,602.176.563·10-19 → 1,602.176.56·10-19 – 9 dígitos
- 1,602.176.563·10-19 → 1,602.176.5·10-19 – 8 dígitos
- 1,602.176.563·10-19 → 1,602.176·10-19 – 7 dígitos
- 1,602.176.563·10-19 → 1,602.17·10-19 – 6 dígitos
- 1,602.176.563·10-19 → 1,602.1·10-19 – 5 dígitos
- 1,602.176.563·10-19 → 1,602·10-19 – 4 dígitos
- 1,602.176.563·10-19 → 1,60·10-19 – 3 dígitos
decimal. Regras de arredondamento:
1 - Se a fração decimal dos dígitos omitidos for maior que 1/2, o dígito menos significativo é aumentado de uma unidade;
2 - Se a fração decimal dos dígitos omitidos for menor que 1/2, o dígito menos significativo permanece inalterado; e
3 - Se a fração decimal dos dígitos omitidos for igual a 1/2, o dígito menos significativo é aumentado de uma unidade caso ele seja ímpar, caso contrário permanece com o mesmo valor.
- Arredondamento para quatro significativos:
0,011.475.0 → 0,011.48 justificativa 0,50 = 1/2 e 7 é ímpar
0,011.465.0 → 0,011.46 justificativa 0,50 = 1/2 e 6 é par
- Arredondamento para três significativos:
0,011.475 → 0,011.5 justificativa 0,75 > 1/2
- Arredondamento para um significativo:
0,011.475 → 0,01 justificativa 0,147.5 < 1/2
Compare o arrendondamento do valor da carga do elétron deste quadro com os resultados de truncamento:
- 1,602.176.563·10-19
- 1,602.176.563·10-19 → 1,602.176.56·10-19 – 9 dígitos
- 1,602.176.563·10-19 → 1,602.176.6·10-19 – 8 dígitos
- 1,602.176.563·10-19 → 1,602.177·10-19 – 7 dígitos
- 1,602.176.563·10-19 → 1,602.18·10-19 – 6 dígitos
- 1,602.176.563·10-19 → 1,602.2·10-19 – 5 dígitos
- 1,602.176.563·10-19 → 1,602·10-19 – 4 dígitos
- 1,602.176.563·10-19 → 1,60·10-19 – 3 dígitos
Segundo Vanin, Gouffon e Helene as regras para o número de algarismos na incerteza padrão de uma medição são:
1 - A incerteza padrão deve ser apresentada com dois algarismos significativos quando o primeiro algarismo significativo do valor da incerteza for o dígito um ou o dígito dois; e
2 - A incerteza padrão pode ser apresentada com um ou dois algarismos significativos quando o primeiro algarismo significativo do valor da incerteza for o dígito três ou maior.
O valor obtido para uma medição foi média de 18,010.200 e incerteza padrão de 0,011.475.
Como a incerteza padrão deve ser apresentada por dois algarismos significativos na situação em que o dígito mais significativo do número é 1 tem-se que:
- incerteza = 0,011 porque no arredondando verifica-se que 0,475 é menor do que 1/2; e
- valor = 18,010 porque no arredondamento para três dígitos após a virgula decimal (mesmo número de dígitos daquele da incerteza) veri fica-se que 0,20 é menor do que 1/2.
* * * * *